FENÔMENOS DE TRANSPORTE
Um bloco cúbico pesando 45 N e com arestas de 250 mm é puxado para cima sobre uma superfície inclinada sobre a qual há uma película fina de óleo SAE 10W a 37 ºC e 3,7x10-2 N.s/m². Se a velocidade do bloco é de 0,6 m/s e a película de óleo tem 0,025 mm de espessura, determine a força requerida para puxar o bloco. Suponha que a distribuição de velocidade na película de óleo seja linear. A superfície está inclinada de 25º a partir da horizontal.
85,55 N
44,15 N
13,22 N
74,51 N
31,52 N
Em uma mineradora água 9810 N/m³ escoa a uma pressão de 280 kPa e com velocidade 5,8 m/s conforme indicação da figura. Determine a pressão e a velocidade no ponto B da tubulação abaixo desconsiderando qualquer perda de energia no trecho.

V = 6,2 m/s; P = 285,15 kPa
V = 17,762 cm/s; P = 285,15 kPa
V = 16 m/s; P = 87,65 kPa
V = 17,762 m/s; P = 149,636 kPa
V = 6,2 cm/s; P = 285,15 kPa
"A pressão ABSOLUTA em gases somente pode ser positiva pois a pressão mínima possível é nula. Entretanto a pressão manométrica (por exemplo a pressão medida em bombas de encher pneu, esfigmomanômetros, ...) pode ser negativa. A pressão manométrica é a diferença de pressão entre o sistema a ser medido e o sistema de referência. Se a pressão manométrica é negativa significa que o sistema medido está a uma pressão inferior à pressão de referência. No interior de tubos de imagem de televisores, lâmpadas etc., a pressão manométrica é negativa. Como usualmente a pressão de referência é a pressão atmosférica, o vácuo (pressão absoluta nula ou desprezível) corresponderia a - 1 atm (menos uma atmosfera)."
https://www.if.ufrgs.br/cref/?area=questions&id=84
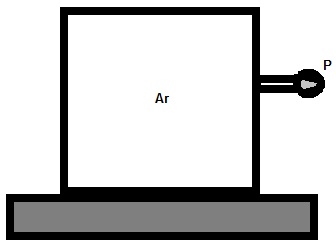
Um indicador de pressão manométrica instalada em um tanque rígido mostra um vácuo de 62 KPa dentro de um tanque como na figura abaixo, situado em um local onde a elevação é de 2000 m e a pressão atmosférica local é de 79,5 KPa. Determine a pressão absoluta dentro do tanque.
17,5 kPa
141,5 kPa
141,5 N/m²
17,5 kfg/cm²
141,5 bar
Determine o coeficiente de difusão binária do O2 no N2 a 320 K e 1 atm: Dado: DO2-N2 = 1,8 x 10-5 m²/s a T1 = 273 K e P1 = 1 atm.
5,02 x 10-5 m2/s
6,03 x 10-5 m2/s
3,27 x 10-5 m2/s
1,42 x 10-5 m2/s
2,28 x 10-5 m2/s
O número de Reynolds é:
Diretamente proporcional ao triplo da velocidade média de escoamento do fluido.
Tem as dimensões da velocidade média do escoamento do fluido.
Adimensional e depende da viscosidade do fluido para realizar o seu cálculo.
Diretamente proporcional ao quadrado da velocidade média de escomento do fluido.
Diretamente proporcional ao quadrado da velocidade média e inversalmente ao diâmetro da tubulação.
A turbobomba da figura abaixo recalca água do reservatório inferior para o reservatório superior a uma taxa de 0,055 m³/s. A tubulação tem seção constante de 60 mm de diâmetro e a perda de carga na tubulação e nas singularidades da tubulação valem 0,8V2/2.g. Determine a potência da bomba necessária para realizar o bombeamento se ela tem rendimento de 84%.

25,64 MW
26,45 kW
50,27 GW
12,45 MW
39,31 kW
A água a 88 ºC é transportada ao longo de uma tubulação de 1500 m de comprimento e 125 mm de diâmetro feita de ferro forjado com vazão de 2 m³/s. Utilizando a equação apresentada por Swamee e Jain abaixo (1976), assinale a alternativa correta que contém a queda de pressão ao longo desta tubulação. Dados: 62,4 N/m³; 10-5 m²/s; rugosidade 0,15 mm.
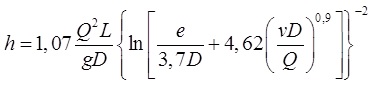
Onde:
L = comprimento da tubulação;
g = aceleração gravitacional;
Q = vazão em m³;
v = viscosidade;
e = rugosidade da tubulação;
h = perda de carga.
4,769 kPa
2,258 kPa
1,523 kPa
5,108 kPa
9,871 kPa
Um grupo de alunos de engenharia realizaram um pré-projeto de uma barragem, neste projeto a entrada da tubulação vai ter uma seção reta de 0,74 m² e a velocidade da água será de 4 m/s. Na saída, a uma altura H = 50 m abaixo da entrada da água na tubulação, a seção da tubulação abaixo do ponto de entrada é reta e menor que a da entrada e a velocidade da água é 20 m/s. Qual é a diferença de pressão em m.c.a entre a entrada e a saída da tubulação? Dado: considere o fluido como água 9810 N/m³; g = 9,816 m/s².
- 5,44 m.c.a
- 88,44 m.c.a
- 50,44 m.c.a
- 30,44 m.c.a
- 552,44 m.c.a
A água peso específico 1000 kgf / m³ circula pela tubulação da figura abaixo onde D1 = 300 mm e D2 = 150 mm. À tubulação está ligado um manômetro de mercúrio cujo peso específico é 13600 kgf/m³. Admitindo que não haja perdas de energia entre (1) e (2), determinar a vazão em volume.
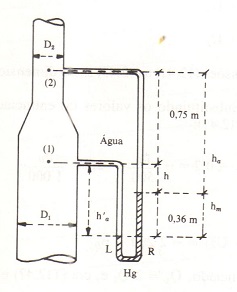
Q = 0,174 m³ / s
Q = 3,25 m³ / s
Q = 10,35 m³ / s
Q = 7,83 m³ / s
Q = 8,25 m³ / s
A pressão sanguínea normal de um ser humano é de 120/80 mmHg. Simulando um manômetro de tubo em U como um esfigmomanômetro (medidor de pressão arterial), a medida desta pressão em unidades do sistema internacional será: Dados: SHg = 13,6, e 9,81 kN/m³.
85,55 N
44,15 N
13,22 N
74,51 N
31,52 N
Em uma mineradora água 9810 N/m³ escoa a uma pressão de 280 kPa e com velocidade 5,8 m/s conforme indicação da figura. Determine a pressão e a velocidade no ponto B da tubulação abaixo desconsiderando qualquer perda de energia no trecho.

V = 6,2 m/s; P = 285,15 kPa
V = 17,762 cm/s; P = 285,15 kPa
V = 16 m/s; P = 87,65 kPa
V = 17,762 m/s; P = 149,636 kPa
V = 6,2 cm/s; P = 285,15 kPa
"A pressão ABSOLUTA em gases somente pode ser positiva pois a pressão mínima possível é nula. Entretanto a pressão manométrica (por exemplo a pressão medida em bombas de encher pneu, esfigmomanômetros, ...) pode ser negativa. A pressão manométrica é a diferença de pressão entre o sistema a ser medido e o sistema de referência. Se a pressão manométrica é negativa significa que o sistema medido está a uma pressão inferior à pressão de referência. No interior de tubos de imagem de televisores, lâmpadas etc., a pressão manométrica é negativa. Como usualmente a pressão de referência é a pressão atmosférica, o vácuo (pressão absoluta nula ou desprezível) corresponderia a - 1 atm (menos uma atmosfera)."
https://www.if.ufrgs.br/cref/?area=questions&id=84
Um indicador de pressão manométrica instalada em um tanque rígido mostra um vácuo de 62 KPa dentro de um tanque como na figura abaixo, situado em um local onde a elevação é de 2000 m e a pressão atmosférica local é de 79,5 KPa. Determine a pressão absoluta dentro do tanque.

17,5 kPa
141,5 kPa
141,5 N/m²
17,5 kfg/cm²
141,5 bar
Determine o coeficiente de difusão binária do O2 no N2 a 320 K e 1 atm: Dado: DO2-N2 = 1,8 x 10-5 m²/s a T1 = 273 K e P1 = 1 atm.
5,02 x 10-5 m2/s
6,03 x 10-5 m2/s
3,27 x 10-5 m2/s
1,42 x 10-5 m2/s
2,28 x 10-5 m2/s
O número de Reynolds é:
Diretamente proporcional ao triplo da velocidade média de escoamento do fluido.
Tem as dimensões da velocidade média do escoamento do fluido.
Adimensional e depende da viscosidade do fluido para realizar o seu cálculo.
Diretamente proporcional ao quadrado da velocidade média de escomento do fluido.
Diretamente proporcional ao quadrado da velocidade média e inversalmente ao diâmetro da tubulação.
A turbobomba da figura abaixo recalca água do reservatório inferior para o reservatório superior a uma taxa de 0,055 m³/s. A tubulação tem seção constante de 60 mm de diâmetro e a perda de carga na tubulação e nas singularidades da tubulação valem 0,8V2/2.g. Determine a potência da bomba necessária para realizar o bombeamento se ela tem rendimento de 84%.

25,64 MW
26,45 kW
50,27 GW
12,45 MW
39,31 kW
A água a 88 ºC é transportada ao longo de uma tubulação de 1500 m de comprimento e 125 mm de diâmetro feita de ferro forjado com vazão de 2 m³/s. Utilizando a equação apresentada por Swamee e Jain abaixo (1976), assinale a alternativa correta que contém a queda de pressão ao longo desta tubulação. Dados: 62,4 N/m³; 10-5 m²/s; rugosidade 0,15 mm.
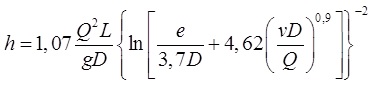
Onde:
L = comprimento da tubulação;
g = aceleração gravitacional;
Q = vazão em m³;
v = viscosidade;
e = rugosidade da tubulação;
h = perda de carga.
4,769 kPa
2,258 kPa
1,523 kPa
5,108 kPa
9,871 kPa
Um grupo de alunos de engenharia realizaram um pré-projeto de uma barragem, neste projeto a entrada da tubulação vai ter uma seção reta de 0,74 m² e a velocidade da água será de 4 m/s. Na saída, a uma altura H = 50 m abaixo da entrada da água na tubulação, a seção da tubulação abaixo do ponto de entrada é reta e menor que a da entrada e a velocidade da água é 20 m/s. Qual é a diferença de pressão em m.c.a entre a entrada e a saída da tubulação? Dado: considere o fluido como água 9810 N/m³; g = 9,816 m/s².
- 5,44 m.c.a
- 88,44 m.c.a
- 50,44 m.c.a
- 30,44 m.c.a
- 552,44 m.c.a
A água peso específico 1000 kgf / m³ circula pela tubulação da figura abaixo onde D1 = 300 mm e D2 = 150 mm. À tubulação está ligado um manômetro de mercúrio cujo peso específico é 13600 kgf/m³. Admitindo que não haja perdas de energia entre (1) e (2), determinar a vazão em volume.

Q = 0,174 m³ / s
Q = 3,25 m³ / s
Q = 10,35 m³ / s
Q = 7,83 m³ / s
Q = 8,25 m³ / s
A pressão sanguínea normal de um ser humano é de 120/80 mmHg. Simulando um manômetro de tubo em U como um esfigmomanômetro (medidor de pressão arterial), a medida desta pressão em unidades do sistema internacional será: Dados: SHg = 13,6, e 9,81 kN/m³.
V = 6,2 m/s; P = 285,15 kPa
V = 17,762 cm/s; P = 285,15 kPa
V = 16 m/s; P = 87,65 kPa
V = 17,762 m/s; P = 149,636 kPa
V = 6,2 cm/s; P = 285,15 kPa
"A pressão ABSOLUTA em gases somente pode ser positiva pois a pressão mínima possível é nula. Entretanto a pressão manométrica (por exemplo a pressão medida em bombas de encher pneu, esfigmomanômetros, ...) pode ser negativa. A pressão manométrica é a diferença de pressão entre o sistema a ser medido e o sistema de referência. Se a pressão manométrica é negativa significa que o sistema medido está a uma pressão inferior à pressão de referência. No interior de tubos de imagem de televisores, lâmpadas etc., a pressão manométrica é negativa. Como usualmente a pressão de referência é a pressão atmosférica, o vácuo (pressão absoluta nula ou desprezível) corresponderia a - 1 atm (menos uma atmosfera)."
https://www.if.ufrgs.br/cref/?area=questions&id=84
Um indicador de pressão manométrica instalada em um tanque rígido mostra um vácuo de 62 KPa dentro de um tanque como na figura abaixo, situado em um local onde a elevação é de 2000 m e a pressão atmosférica local é de 79,5 KPa. Determine a pressão absoluta dentro do tanque.

17,5 kPa
141,5 kPa
141,5 N/m²
17,5 kfg/cm²
141,5 bar
Determine o coeficiente de difusão binária do O2 no N2 a 320 K e 1 atm: Dado: DO2-N2 = 1,8 x 10-5 m²/s a T1 = 273 K e P1 = 1 atm.
5,02 x 10-5 m2/s
6,03 x 10-5 m2/s
3,27 x 10-5 m2/s
1,42 x 10-5 m2/s
2,28 x 10-5 m2/s
O número de Reynolds é:
Diretamente proporcional ao triplo da velocidade média de escoamento do fluido.
Tem as dimensões da velocidade média do escoamento do fluido.
Adimensional e depende da viscosidade do fluido para realizar o seu cálculo.
Diretamente proporcional ao quadrado da velocidade média de escomento do fluido.
Diretamente proporcional ao quadrado da velocidade média e inversalmente ao diâmetro da tubulação.
A turbobomba da figura abaixo recalca água do reservatório inferior para o reservatório superior a uma taxa de 0,055 m³/s. A tubulação tem seção constante de 60 mm de diâmetro e a perda de carga na tubulação e nas singularidades da tubulação valem 0,8V2/2.g. Determine a potência da bomba necessária para realizar o bombeamento se ela tem rendimento de 84%.

25,64 MW
26,45 kW
50,27 GW
12,45 MW
39,31 kW
A água a 88 ºC é transportada ao longo de uma tubulação de 1500 m de comprimento e 125 mm de diâmetro feita de ferro forjado com vazão de 2 m³/s. Utilizando a equação apresentada por Swamee e Jain abaixo (1976), assinale a alternativa correta que contém a queda de pressão ao longo desta tubulação. Dados: 62,4 N/m³; 10-5 m²/s; rugosidade 0,15 mm.
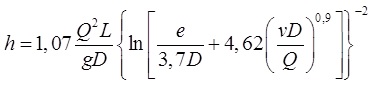
Onde:
L = comprimento da tubulação;
g = aceleração gravitacional;
Q = vazão em m³;
v = viscosidade;
e = rugosidade da tubulação;
h = perda de carga.
4,769 kPa
2,258 kPa
1,523 kPa
5,108 kPa
9,871 kPa
Um grupo de alunos de engenharia realizaram um pré-projeto de uma barragem, neste projeto a entrada da tubulação vai ter uma seção reta de 0,74 m² e a velocidade da água será de 4 m/s. Na saída, a uma altura H = 50 m abaixo da entrada da água na tubulação, a seção da tubulação abaixo do ponto de entrada é reta e menor que a da entrada e a velocidade da água é 20 m/s. Qual é a diferença de pressão em m.c.a entre a entrada e a saída da tubulação? Dado: considere o fluido como água 9810 N/m³; g = 9,816 m/s².
- 5,44 m.c.a
- 88,44 m.c.a
- 50,44 m.c.a
- 30,44 m.c.a
- 552,44 m.c.a
A água peso específico 1000 kgf / m³ circula pela tubulação da figura abaixo onde D1 = 300 mm e D2 = 150 mm. À tubulação está ligado um manômetro de mercúrio cujo peso específico é 13600 kgf/m³. Admitindo que não haja perdas de energia entre (1) e (2), determinar a vazão em volume.

Q = 0,174 m³ / s
Q = 3,25 m³ / s
Q = 10,35 m³ / s
Q = 7,83 m³ / s
Q = 8,25 m³ / s
A pressão sanguínea normal de um ser humano é de 120/80 mmHg. Simulando um manômetro de tubo em U como um esfigmomanômetro (medidor de pressão arterial), a medida desta pressão em unidades do sistema internacional será: Dados: SHg = 13,6, e 9,81 kN/m³.

17,5 kPa
141,5 kPa
141,5 N/m²
17,5 kfg/cm²
141,5 bar
Determine o coeficiente de difusão binária do O2 no N2 a 320 K e 1 atm: Dado: DO2-N2 = 1,8 x 10-5 m²/s a T1 = 273 K e P1 = 1 atm.
5,02 x 10-5 m2/s
6,03 x 10-5 m2/s
3,27 x 10-5 m2/s
1,42 x 10-5 m2/s
2,28 x 10-5 m2/s
O número de Reynolds é:
Diretamente proporcional ao triplo da velocidade média de escoamento do fluido.
Tem as dimensões da velocidade média do escoamento do fluido.
Adimensional e depende da viscosidade do fluido para realizar o seu cálculo.
Diretamente proporcional ao quadrado da velocidade média de escomento do fluido.
Diretamente proporcional ao quadrado da velocidade média e inversalmente ao diâmetro da tubulação.
A turbobomba da figura abaixo recalca água do reservatório inferior para o reservatório superior a uma taxa de 0,055 m³/s. A tubulação tem seção constante de 60 mm de diâmetro e a perda de carga na tubulação e nas singularidades da tubulação valem 0,8V2/2.g. Determine a potência da bomba necessária para realizar o bombeamento se ela tem rendimento de 84%.

25,64 MW
26,45 kW
50,27 GW
12,45 MW
39,31 kW
A água a 88 ºC é transportada ao longo de uma tubulação de 1500 m de comprimento e 125 mm de diâmetro feita de ferro forjado com vazão de 2 m³/s. Utilizando a equação apresentada por Swamee e Jain abaixo (1976), assinale a alternativa correta que contém a queda de pressão ao longo desta tubulação. Dados: 62,4 N/m³; 10-5 m²/s; rugosidade 0,15 mm.
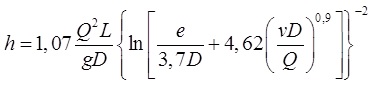
Onde:
L = comprimento da tubulação;
g = aceleração gravitacional;
Q = vazão em m³;
v = viscosidade;
e = rugosidade da tubulação;
h = perda de carga.
4,769 kPa
2,258 kPa
1,523 kPa
5,108 kPa
9,871 kPa
Um grupo de alunos de engenharia realizaram um pré-projeto de uma barragem, neste projeto a entrada da tubulação vai ter uma seção reta de 0,74 m² e a velocidade da água será de 4 m/s. Na saída, a uma altura H = 50 m abaixo da entrada da água na tubulação, a seção da tubulação abaixo do ponto de entrada é reta e menor que a da entrada e a velocidade da água é 20 m/s. Qual é a diferença de pressão em m.c.a entre a entrada e a saída da tubulação? Dado: considere o fluido como água 9810 N/m³; g = 9,816 m/s².
- 5,44 m.c.a
- 88,44 m.c.a
- 50,44 m.c.a
- 30,44 m.c.a
- 552,44 m.c.a
A água peso específico 1000 kgf / m³ circula pela tubulação da figura abaixo onde D1 = 300 mm e D2 = 150 mm. À tubulação está ligado um manômetro de mercúrio cujo peso específico é 13600 kgf/m³. Admitindo que não haja perdas de energia entre (1) e (2), determinar a vazão em volume.

Q = 0,174 m³ / s
Q = 3,25 m³ / s
Q = 10,35 m³ / s
Q = 7,83 m³ / s
Q = 8,25 m³ / s
A pressão sanguínea normal de um ser humano é de 120/80 mmHg. Simulando um manômetro de tubo em U como um esfigmomanômetro (medidor de pressão arterial), a medida desta pressão em unidades do sistema internacional será: Dados: SHg = 13,6, e 9,81 kN/m³.
5,02 x 10-5 m2/s
6,03 x 10-5 m2/s
3,27 x 10-5 m2/s
1,42 x 10-5 m2/s
2,28 x 10-5 m2/s
O número de Reynolds é:
Diretamente proporcional ao triplo da velocidade média de escoamento do fluido.
Tem as dimensões da velocidade média do escoamento do fluido.
Adimensional e depende da viscosidade do fluido para realizar o seu cálculo.
Diretamente proporcional ao quadrado da velocidade média de escomento do fluido.
Diretamente proporcional ao quadrado da velocidade média e inversalmente ao diâmetro da tubulação.
A turbobomba da figura abaixo recalca água do reservatório inferior para o reservatório superior a uma taxa de 0,055 m³/s. A tubulação tem seção constante de 60 mm de diâmetro e a perda de carga na tubulação e nas singularidades da tubulação valem 0,8V2/2.g. Determine a potência da bomba necessária para realizar o bombeamento se ela tem rendimento de 84%.

25,64 MW
26,45 kW
50,27 GW
12,45 MW
39,31 kW
A água a 88 ºC é transportada ao longo de uma tubulação de 1500 m de comprimento e 125 mm de diâmetro feita de ferro forjado com vazão de 2 m³/s. Utilizando a equação apresentada por Swamee e Jain abaixo (1976), assinale a alternativa correta que contém a queda de pressão ao longo desta tubulação. Dados: 62,4 N/m³; 10-5 m²/s; rugosidade 0,15 mm.
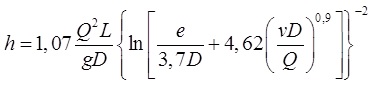
Onde:
L = comprimento da tubulação;
g = aceleração gravitacional;
Q = vazão em m³;
v = viscosidade;
e = rugosidade da tubulação;
h = perda de carga.
4,769 kPa
2,258 kPa
1,523 kPa
5,108 kPa
9,871 kPa
Um grupo de alunos de engenharia realizaram um pré-projeto de uma barragem, neste projeto a entrada da tubulação vai ter uma seção reta de 0,74 m² e a velocidade da água será de 4 m/s. Na saída, a uma altura H = 50 m abaixo da entrada da água na tubulação, a seção da tubulação abaixo do ponto de entrada é reta e menor que a da entrada e a velocidade da água é 20 m/s. Qual é a diferença de pressão em m.c.a entre a entrada e a saída da tubulação? Dado: considere o fluido como água 9810 N/m³; g = 9,816 m/s².
- 5,44 m.c.a
- 88,44 m.c.a
- 50,44 m.c.a
- 30,44 m.c.a
- 552,44 m.c.a
A água peso específico 1000 kgf / m³ circula pela tubulação da figura abaixo onde D1 = 300 mm e D2 = 150 mm. À tubulação está ligado um manômetro de mercúrio cujo peso específico é 13600 kgf/m³. Admitindo que não haja perdas de energia entre (1) e (2), determinar a vazão em volume.

Q = 0,174 m³ / s
Q = 3,25 m³ / s
Q = 10,35 m³ / s
Q = 7,83 m³ / s
Q = 8,25 m³ / s
A pressão sanguínea normal de um ser humano é de 120/80 mmHg. Simulando um manômetro de tubo em U como um esfigmomanômetro (medidor de pressão arterial), a medida desta pressão em unidades do sistema internacional será: Dados: SHg = 13,6, e 9,81 kN/m³.
Diretamente proporcional ao triplo da velocidade média de escoamento do fluido.
Tem as dimensões da velocidade média do escoamento do fluido.
Adimensional e depende da viscosidade do fluido para realizar o seu cálculo.
Diretamente proporcional ao quadrado da velocidade média de escomento do fluido.
Diretamente proporcional ao quadrado da velocidade média e inversalmente ao diâmetro da tubulação.
A turbobomba da figura abaixo recalca água do reservatório inferior para o reservatório superior a uma taxa de 0,055 m³/s. A tubulação tem seção constante de 60 mm de diâmetro e a perda de carga na tubulação e nas singularidades da tubulação valem 0,8V2/2.g. Determine a potência da bomba necessária para realizar o bombeamento se ela tem rendimento de 84%.

25,64 MW
26,45 kW
50,27 GW
12,45 MW
39,31 kW
A água a 88 ºC é transportada ao longo de uma tubulação de 1500 m de comprimento e 125 mm de diâmetro feita de ferro forjado com vazão de 2 m³/s. Utilizando a equação apresentada por Swamee e Jain abaixo (1976), assinale a alternativa correta que contém a queda de pressão ao longo desta tubulação. Dados: 62,4 N/m³; 10-5 m²/s; rugosidade 0,15 mm.
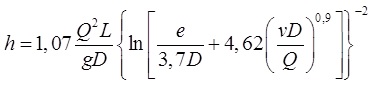
Onde:
L = comprimento da tubulação;
g = aceleração gravitacional;
Q = vazão em m³;
v = viscosidade;
e = rugosidade da tubulação;
h = perda de carga.
4,769 kPa
2,258 kPa
1,523 kPa
5,108 kPa
9,871 kPa
Um grupo de alunos de engenharia realizaram um pré-projeto de uma barragem, neste projeto a entrada da tubulação vai ter uma seção reta de 0,74 m² e a velocidade da água será de 4 m/s. Na saída, a uma altura H = 50 m abaixo da entrada da água na tubulação, a seção da tubulação abaixo do ponto de entrada é reta e menor que a da entrada e a velocidade da água é 20 m/s. Qual é a diferença de pressão em m.c.a entre a entrada e a saída da tubulação? Dado: considere o fluido como água 9810 N/m³; g = 9,816 m/s².
- 5,44 m.c.a
- 88,44 m.c.a
- 50,44 m.c.a
- 30,44 m.c.a
- 552,44 m.c.a
A água peso específico 1000 kgf / m³ circula pela tubulação da figura abaixo onde D1 = 300 mm e D2 = 150 mm. À tubulação está ligado um manômetro de mercúrio cujo peso específico é 13600 kgf/m³. Admitindo que não haja perdas de energia entre (1) e (2), determinar a vazão em volume.

Q = 0,174 m³ / s
Q = 3,25 m³ / s
Q = 10,35 m³ / s
Q = 7,83 m³ / s
Q = 8,25 m³ / s
A pressão sanguínea normal de um ser humano é de 120/80 mmHg. Simulando um manômetro de tubo em U como um esfigmomanômetro (medidor de pressão arterial), a medida desta pressão em unidades do sistema internacional será: Dados: SHg = 13,6, e 9,81 kN/m³.
25,64 MW
26,45 kW
50,27 GW
12,45 MW
39,31 kW
A água a 88 ºC é transportada ao longo de uma tubulação de 1500 m de comprimento e 125 mm de diâmetro feita de ferro forjado com vazão de 2 m³/s. Utilizando a equação apresentada por Swamee e Jain abaixo (1976), assinale a alternativa correta que contém a queda de pressão ao longo desta tubulação. Dados: 62,4 N/m³; 10-5 m²/s; rugosidade 0,15 mm.
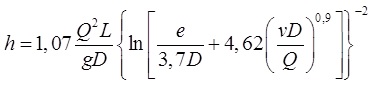
Onde:
L = comprimento da tubulação;
g = aceleração gravitacional;
Q = vazão em m³;
v = viscosidade;
e = rugosidade da tubulação;
h = perda de carga.
4,769 kPa
2,258 kPa
1,523 kPa
5,108 kPa
9,871 kPa
Um grupo de alunos de engenharia realizaram um pré-projeto de uma barragem, neste projeto a entrada da tubulação vai ter uma seção reta de 0,74 m² e a velocidade da água será de 4 m/s. Na saída, a uma altura H = 50 m abaixo da entrada da água na tubulação, a seção da tubulação abaixo do ponto de entrada é reta e menor que a da entrada e a velocidade da água é 20 m/s. Qual é a diferença de pressão em m.c.a entre a entrada e a saída da tubulação? Dado: considere o fluido como água 9810 N/m³; g = 9,816 m/s².
- 5,44 m.c.a
- 88,44 m.c.a
- 50,44 m.c.a
- 30,44 m.c.a
- 552,44 m.c.a
A água peso específico 1000 kgf / m³ circula pela tubulação da figura abaixo onde D1 = 300 mm e D2 = 150 mm. À tubulação está ligado um manômetro de mercúrio cujo peso específico é 13600 kgf/m³. Admitindo que não haja perdas de energia entre (1) e (2), determinar a vazão em volume.

Q = 0,174 m³ / s
Q = 3,25 m³ / s
Q = 10,35 m³ / s
Q = 7,83 m³ / s
Q = 8,25 m³ / s
A pressão sanguínea normal de um ser humano é de 120/80 mmHg. Simulando um manômetro de tubo em U como um esfigmomanômetro (medidor de pressão arterial), a medida desta pressão em unidades do sistema internacional será: Dados: SHg = 13,6, e 9,81 kN/m³.
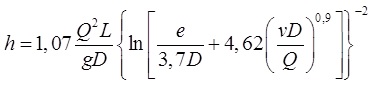
4,769 kPa
2,258 kPa
1,523 kPa
5,108 kPa
9,871 kPa
Um grupo de alunos de engenharia realizaram um pré-projeto de uma barragem, neste projeto a entrada da tubulação vai ter uma seção reta de 0,74 m² e a velocidade da água será de 4 m/s. Na saída, a uma altura H = 50 m abaixo da entrada da água na tubulação, a seção da tubulação abaixo do ponto de entrada é reta e menor que a da entrada e a velocidade da água é 20 m/s. Qual é a diferença de pressão em m.c.a entre a entrada e a saída da tubulação? Dado: considere o fluido como água 9810 N/m³; g = 9,816 m/s².
- 5,44 m.c.a
- 88,44 m.c.a
- 50,44 m.c.a
- 30,44 m.c.a
- 552,44 m.c.a
A água peso específico 1000 kgf / m³ circula pela tubulação da figura abaixo onde D1 = 300 mm e D2 = 150 mm. À tubulação está ligado um manômetro de mercúrio cujo peso específico é 13600 kgf/m³. Admitindo que não haja perdas de energia entre (1) e (2), determinar a vazão em volume.

Q = 0,174 m³ / s
Q = 3,25 m³ / s
Q = 10,35 m³ / s
Q = 7,83 m³ / s
Q = 8,25 m³ / s
A pressão sanguínea normal de um ser humano é de 120/80 mmHg. Simulando um manômetro de tubo em U como um esfigmomanômetro (medidor de pressão arterial), a medida desta pressão em unidades do sistema internacional será: Dados: SHg = 13,6, e 9,81 kN/m³.
- 5,44 m.c.a
- 88,44 m.c.a
- 50,44 m.c.a
- 30,44 m.c.a
- 552,44 m.c.a
A água peso específico 1000 kgf / m³ circula pela tubulação da figura abaixo onde D1 = 300 mm e D2 = 150 mm. À tubulação está ligado um manômetro de mercúrio cujo peso específico é 13600 kgf/m³. Admitindo que não haja perdas de energia entre (1) e (2), determinar a vazão em volume.

Q = 0,174 m³ / s
Q = 3,25 m³ / s
Q = 10,35 m³ / s
Q = 7,83 m³ / s
Q = 8,25 m³ / s
A pressão sanguínea normal de um ser humano é de 120/80 mmHg. Simulando um manômetro de tubo em U como um esfigmomanômetro (medidor de pressão arterial), a medida desta pressão em unidades do sistema internacional será: Dados: SHg = 13,6, e 9,81 kN/m³.

Q = 0,174 m³ / s
Q = 3,25 m³ / s
Q = 10,35 m³ / s
Q = 7,83 m³ / s
Q = 8,25 m³ / s